[5주 차] - 부울 대수(Boolean Algebra), 드모르간의 법칙(De Morgan's Law)
과목명 : 논리회로 실습(Logic circuit practice)
수업일자 : 2022년 09월 27일 (화)
1. 부울 대수(Boolean Algebra)
1-1. 정의
- 부울 대수(Boolean Algebra)는 논리적 공리들을 만족시키는 논리곱, 논리합, 부정의 연산이 정의된 대수 구조입니다.
1-2. 부울 대수의 기본 법칙
- 부울 대수의 모든 항목은 0 또는 1을 가지며 기본 AND, OR 연산의 부울 대수 공리는 아래 정리와 같습니다.
(1) 기본 법칙

(2) 보수성의 법칙(Complement law)

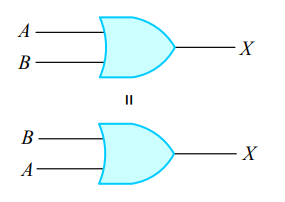
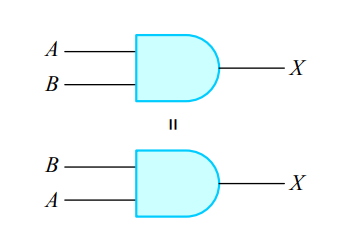
(3) 교환 법칙(Commutative law)

(4) 결합 법칙(Associative law)

(5) 분배 법칙(Distributive law)

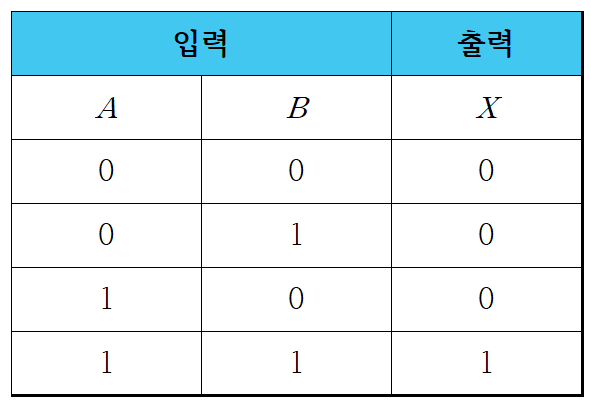
(6) 흡수 법칙(Absorptive law)

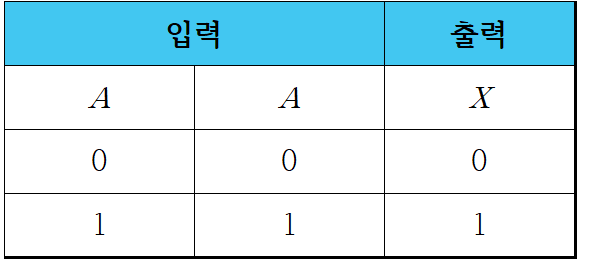
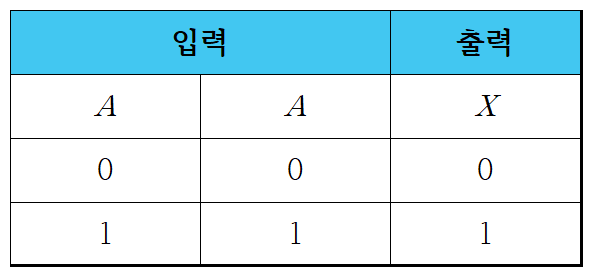
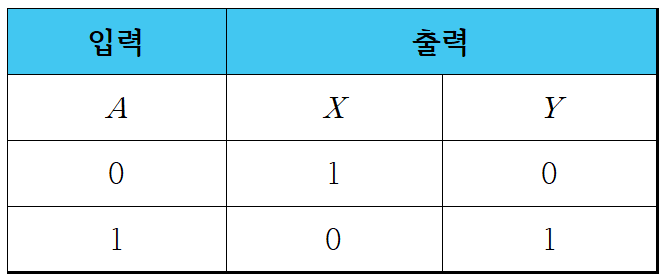
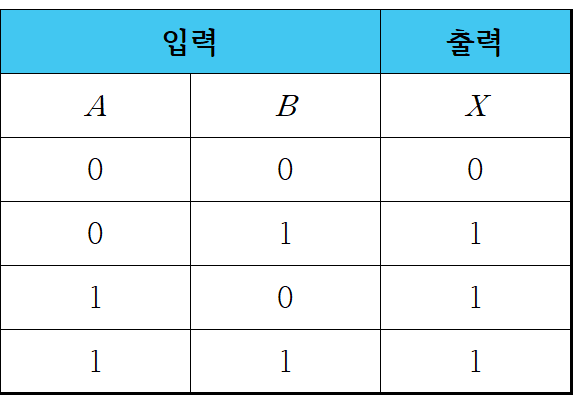
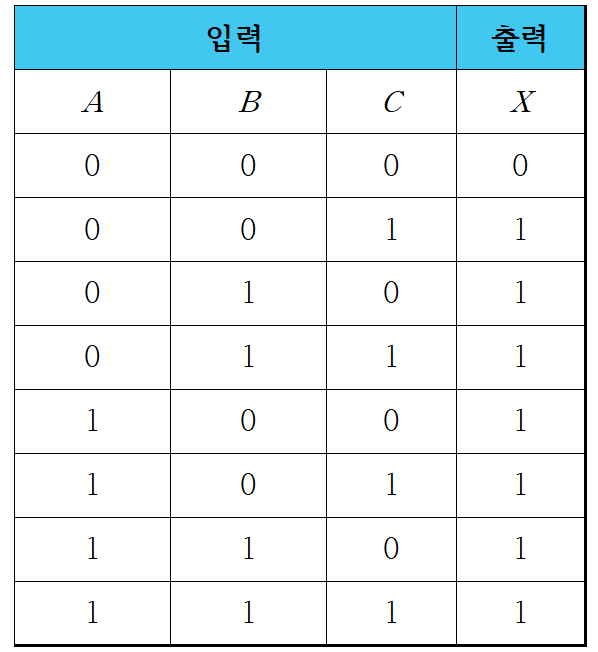
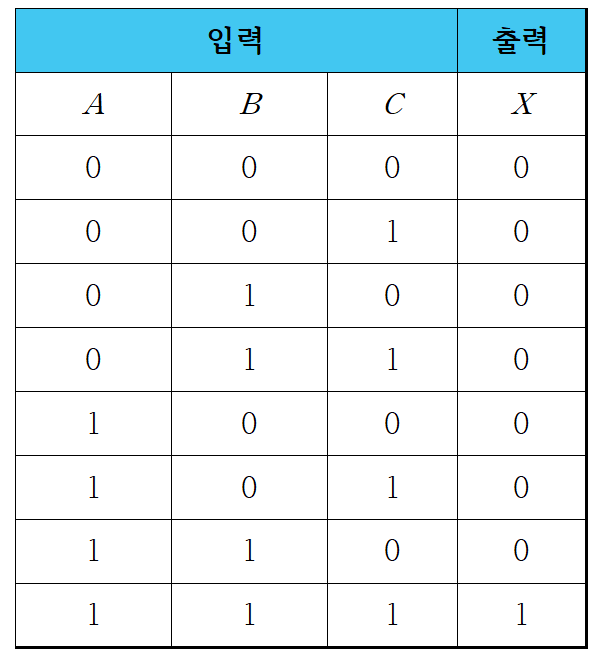
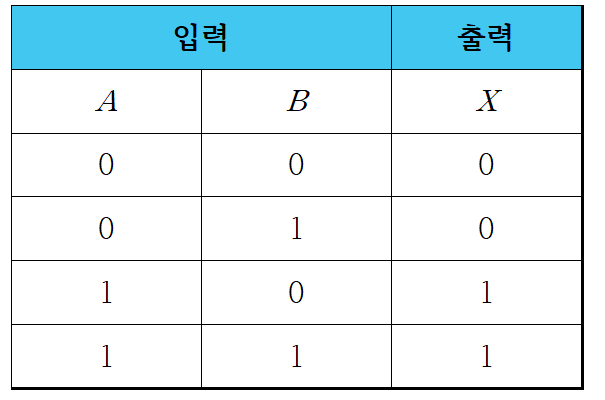
1-3. 진리표를 이용한 분배 법칙 증명
- 위에서 소개된 분배 법칙은 아래의 진리표(Truth table)을 작성함으로써 증명할 수 있습니다.


1-4. 부울 대수를 이용하여 증명 (흡수 법칙)
- 위에서 소개된 흡수 법칙도 부울 대수의 대수적인 성질을 이용하여 증명할 수 있습니다.

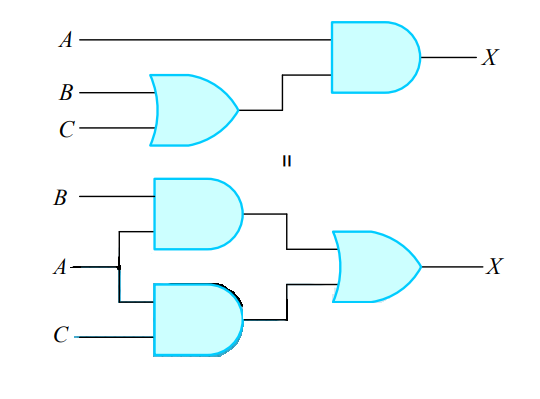
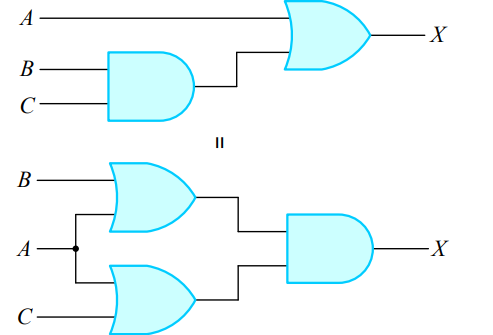
1-5. 부울 대수식의 논리 회로 표현
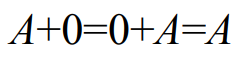
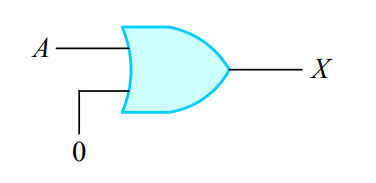
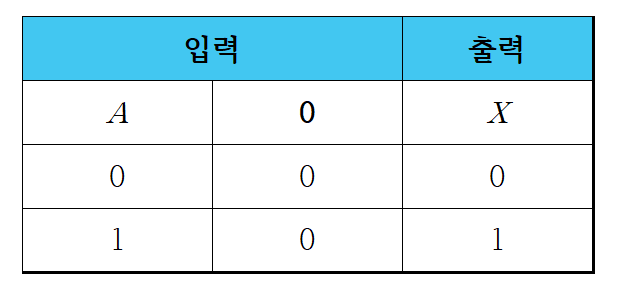
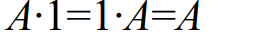
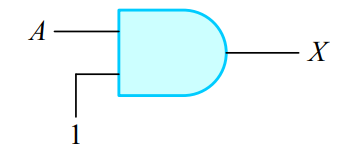
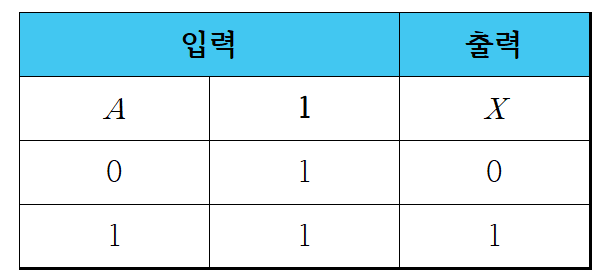
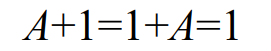
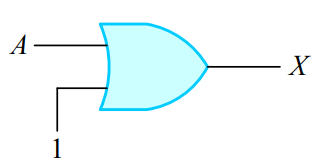
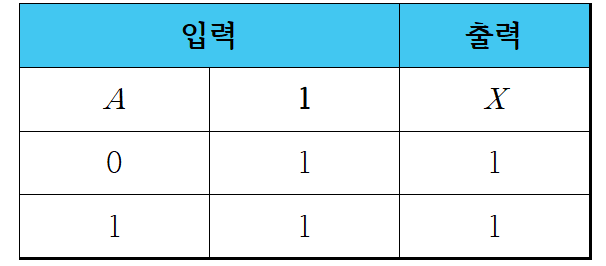
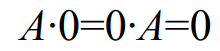
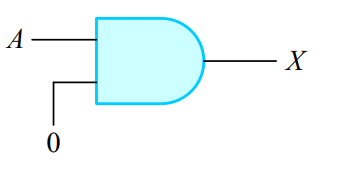
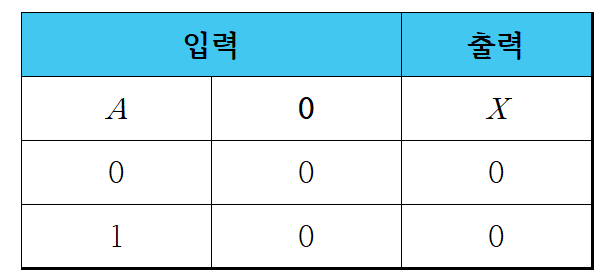
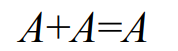
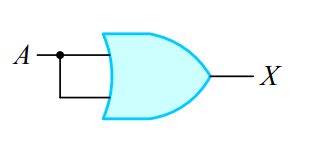
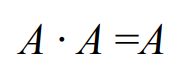
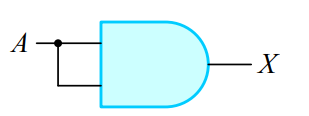
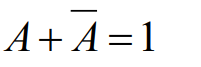
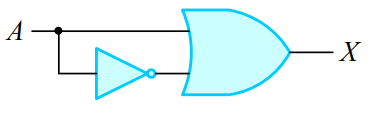
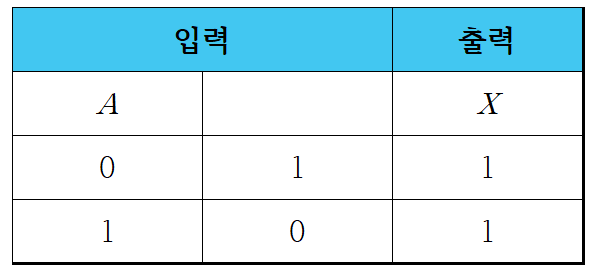
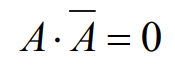
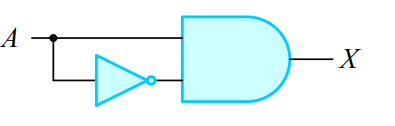
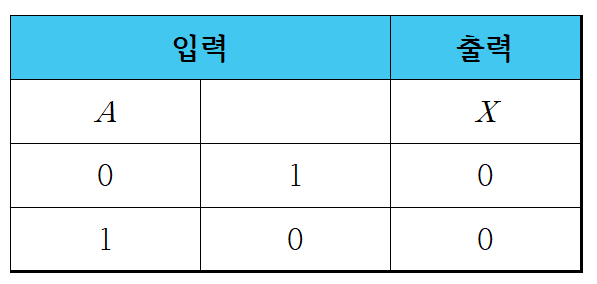
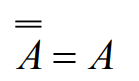
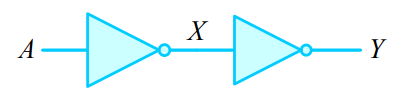
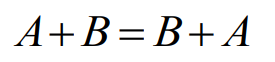
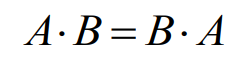
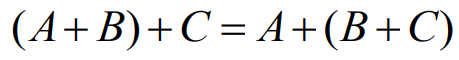
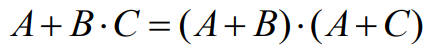
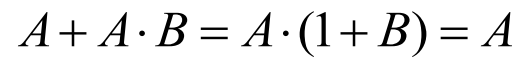
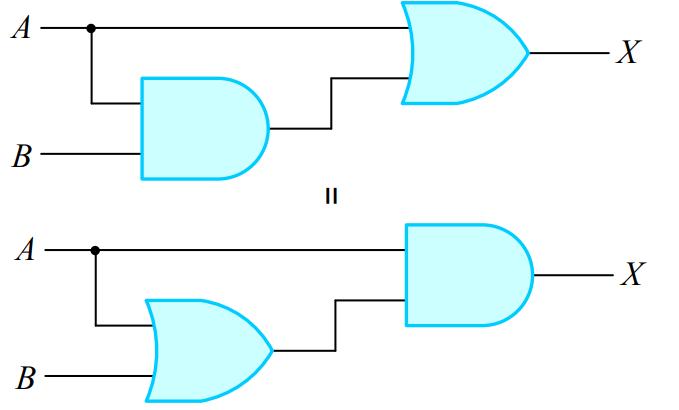
2. 드모르간의 법칙(De Morgan's law)
- 드모르간의 법칙은 수리 논리학, 집합론에서 논리곱, 논리합, 부정 연산 간의 관계를 기술하여 정리한 법칙을 의미합니다.
- 일반적으로 부울식의 보수식을 얻기 위해 사용됩니다.
- 드모르간 법칙의 일반화된 형식은 AND, OR 연산자를 서로 바꾸고 각 리터럴을 보수화함으로써 얻어진다는 사실을 알 수 있습니다.

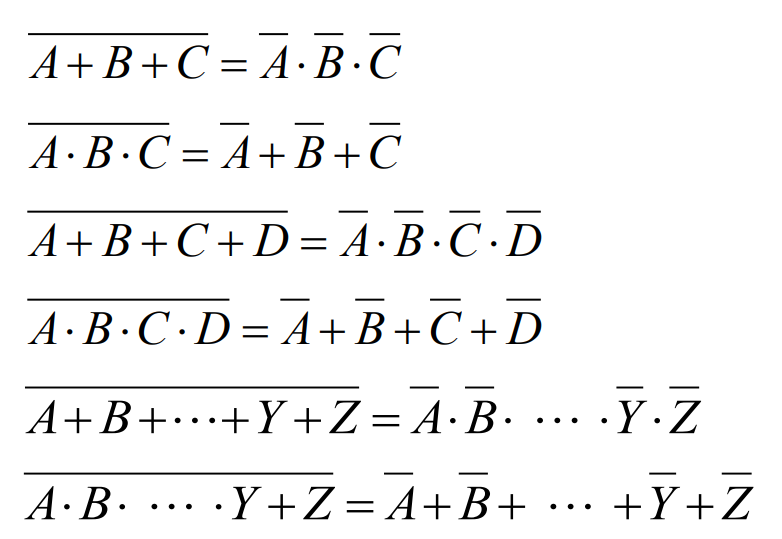
3. 회로 실습 및 Simulation
(1)
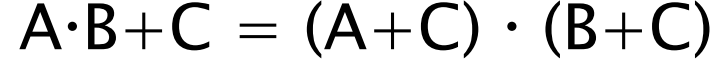
(1-a) 위의 논리식에 대한 회로도 설계하기
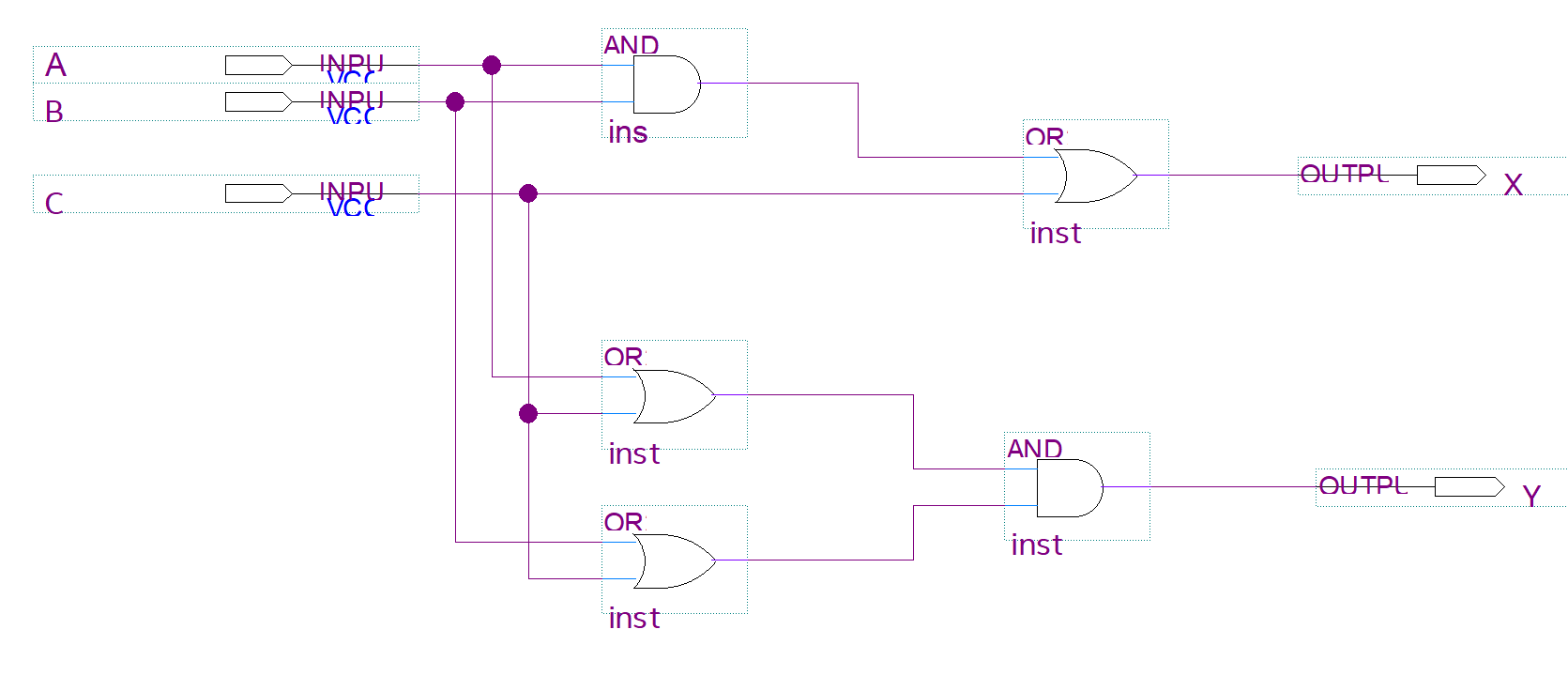
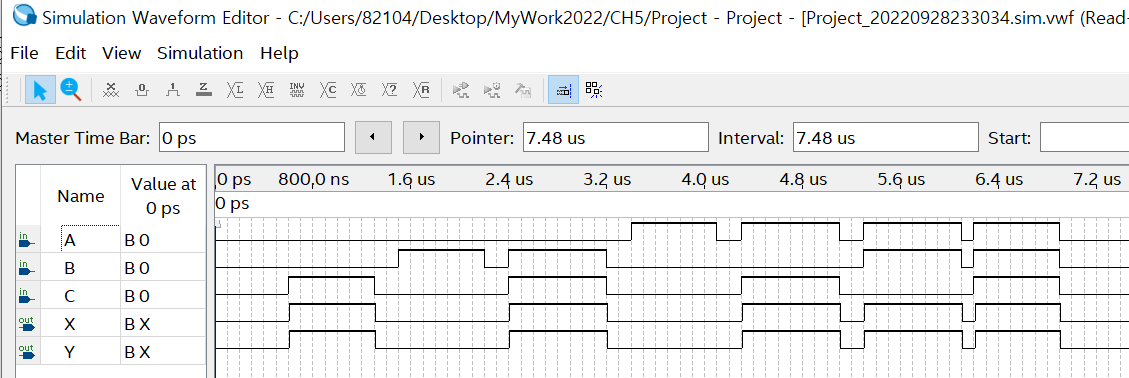
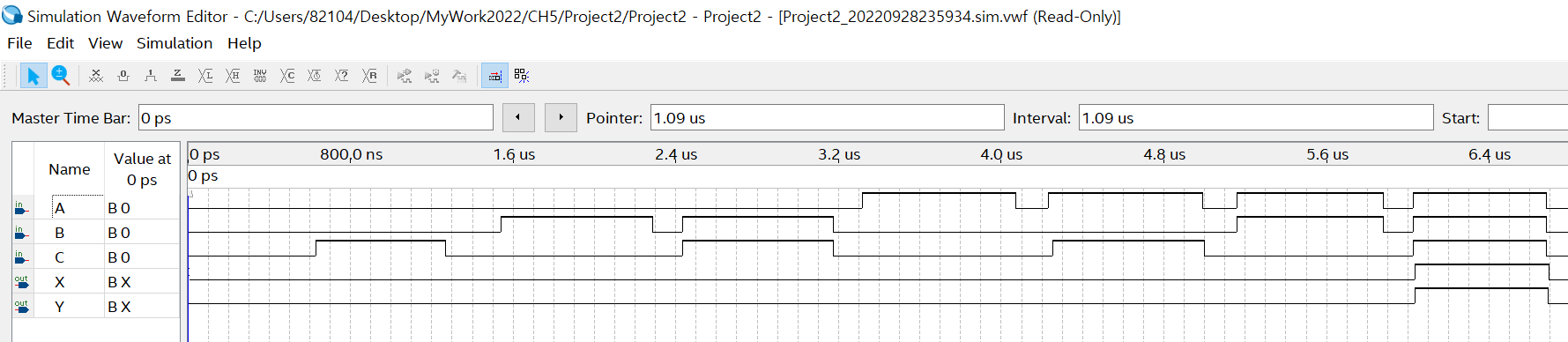
(1-b) 설계된 회로에 대한 Simulation 결과 확인하기
(2)
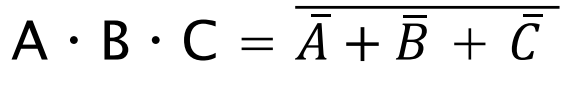
(2-a) 위의 논리식에 대한 회로도 설계하기
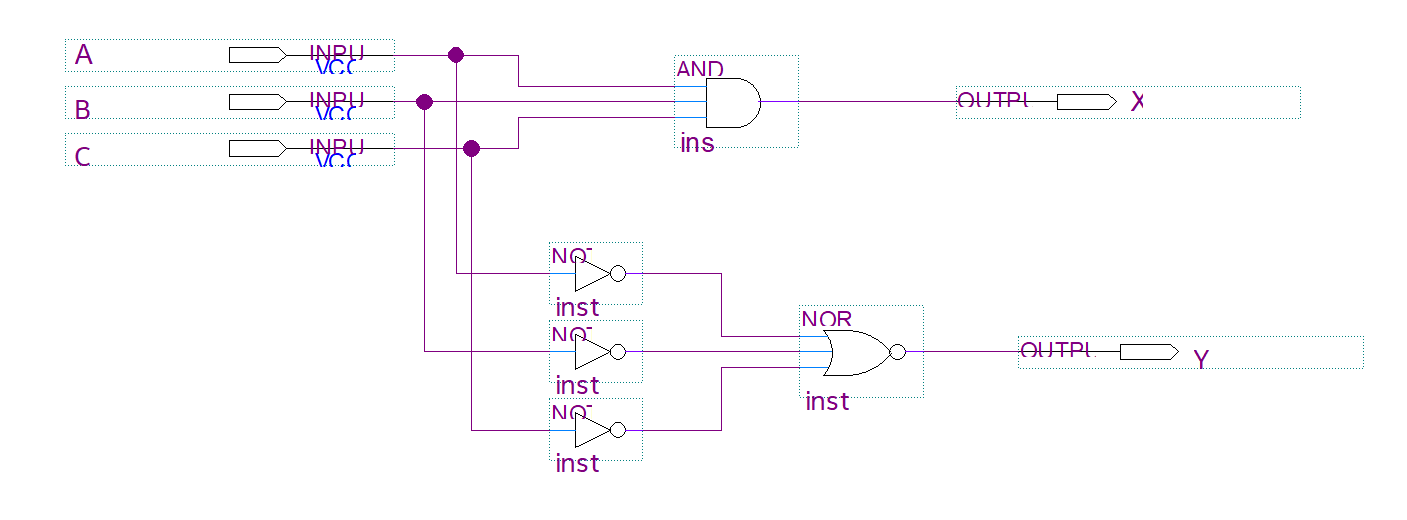
(2-b) 설계된 회로에 대한 Simulation 결과 확인하기
- 학부에서 수강했던 전공 수업 내용을 정리하는 포스팅입니다.
- 내용 중에서 오타 또는 잘못된 내용이 있을 시 지적해 주시기 바랍니다.