[6주 차] - XOR, XNOR 게이트, 논리 함수 간소화
과목명 : 논리회로 실습(Logic circuit practice)
수업일자 : 2022년 10월 04일 (화)
1. XOR 게이트(Exclusive OR Gate)
1-1. 정의와 특징
- XOR(Exclusive OR) 게이트는 베타적 OR 게이트 또는 배타적 논리합(Exclusive logical sum)이라고도 하며 1을 홀수 개 입력하면 1을 출력하고 짝수 개 입력하면 0을 출력합니다.
- 두 개의 입력에 대해 입력값이 같으면 0, 다르면 1을 출력하게 됩니다.
- 짝수 패리티(Even parity)를 구현할 때 주로 사용합니다.
1-2. 2입력 XOR 게이트


1-3. 3입력 XOR 게이트


2. XNOR 게이트(Exclusive NOR Gate)
2-1. 정의와 특징
- XNOR 게이트(Exclusive NOR Gate)는 1을 홀수 개 입력하면 0, 짝수 개 입력하면 1을 출력합니다.
- 홀수 패리티(Odd parity)를 구현할 때 주로 사용합니다.
2-2. 2입력 XNOR 게이트



2-3. 3입력 XNOR 게이트
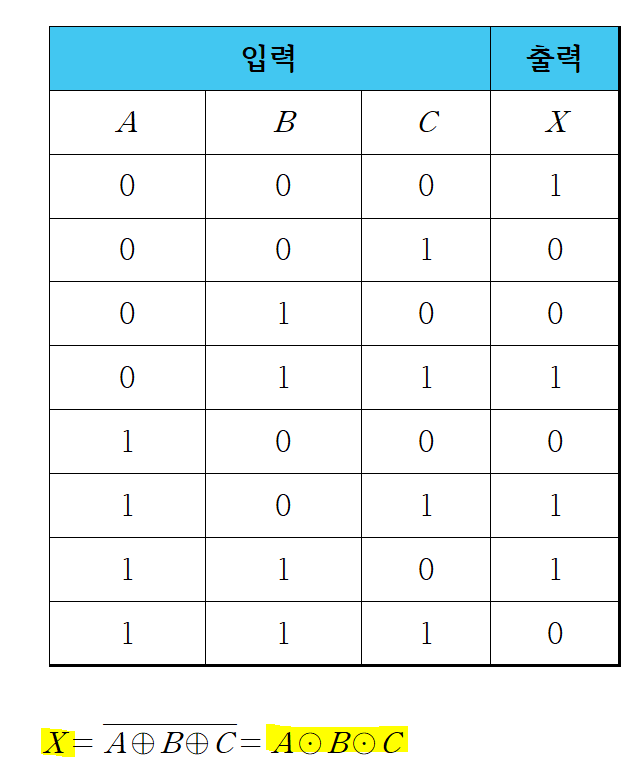

2-4. XOR, XNOR 게이트의 응용
(1) 비교기(Comparator)
- 2진 비교기는 두 2진수 값의 크기를 비교하는 회로입니다.


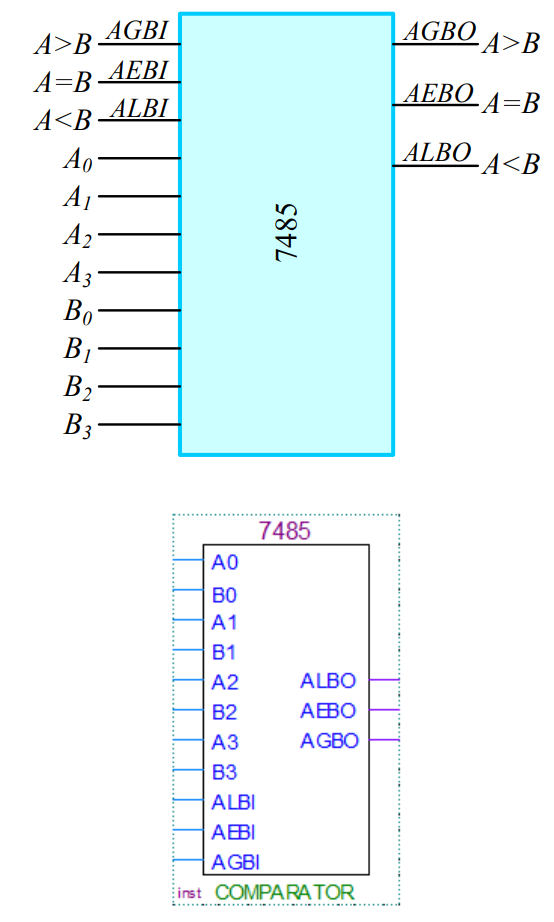
(2) 7485 비교기
- 4비트 2진수 2개를 비교하는 비교기입니다.
- 4비트 비교기의 확장은 두 수가 같은지 다른지 비교할 수 있을 뿐만이 아니라, 어느 수가 더 큰지까지 확인할 수 있는 여부까지 확장할 수 있습니다.
(3) 보수기(XOR 게이트 이용)
- 2진수의 보수에는 1의 보수와 2의 보수가 존재합니다.
- 1의 보수는 0을 1로, 1을 0으로 바꾸면 되며, 2의 보수는 1의 보수 결과의 끝 자리 수에 1을 더하면 됩니다.
- 보수를 사용하는 이유는 뺄셈을 용이하게 하기 위해서 사용됩니다.
- 2진수에서 1의 보수를 만드는 방법은, XOR 게이트의 원리를 통해 쉽게 만들 수 있습니다.
- 1의 보수를 취하고자 하는 경우 : 각 자리(비트)에 1을 XOR한다.
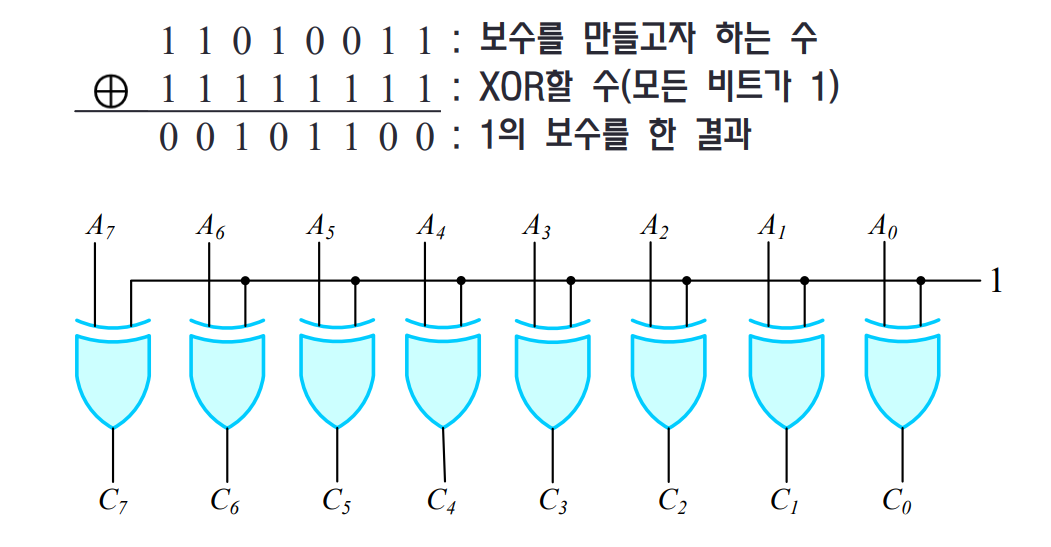
- 위의 원리를 이용하여 2진수를 가지는 특정한 비트에 대해 보수화가 필요하다면 1을 XOR하고, 보수화가 필요하지 않다면 0을 XOR합니다.
(4) 패리티 비트 발생기
- 짝수 패리티(Even parity) - Parity bit를 추가하여 1의 개수를 짝수 개로 만듭니다.
- 홀수 패리티(Odd parity) - Parity bit를 추가하여 1의 개수를 홀수 개로 만듭니다.
3. 논리 함수(부울 함수) 간소화(Simplification)
3-1. 정의
- 논리 함수(부울 함수)를 간소화(Simplification)한다는 것은, 모든 입력과 출력 조건이 동일한 경우에 가능한 부울식을 간소화하여 회로 설계에 이용되는 Term(사용되는 게이트의 수), Literal(게이트의 입력 수)을 최소화하는 것을 말하며 이를 통해 구현 회로의 동작 성능 향상, 가격 절감 등의 효과를 가져올 수 있습니다.
3-2. 여러 가지 간소화 방법
- 논리 회로를 부울 함수로 표현한 후, 부울 함수를 간소화합니다.
(1) 부울 대수(Boolean algebra)의 대수적인 기본 정리를 이용하는 방법
(2) 드모르간의 정리와 SOP, POS 등을 이용하여 공통 인수를 찾고 이를 소거
(3) 카르노 맵(Karnaugh map) 방법
3-3. 최소항과 SOP(Sum of product, 곱의 합)
(1) 정의와 여러 가지 특징
- 최소항(Minterm)은 표준 곱의 항, 즉 함수의 모든 변수를 포함하는 AND 항을 의미합니다.
- 최소항식은 출력이 1이 되는 각 항을 AND로 나타낸 후 OR 연산으로 결합합니다.
- 이때 간소화 여부와 관계없이 AND-OR 식을 SOP라고 합니다.
(2) 예시
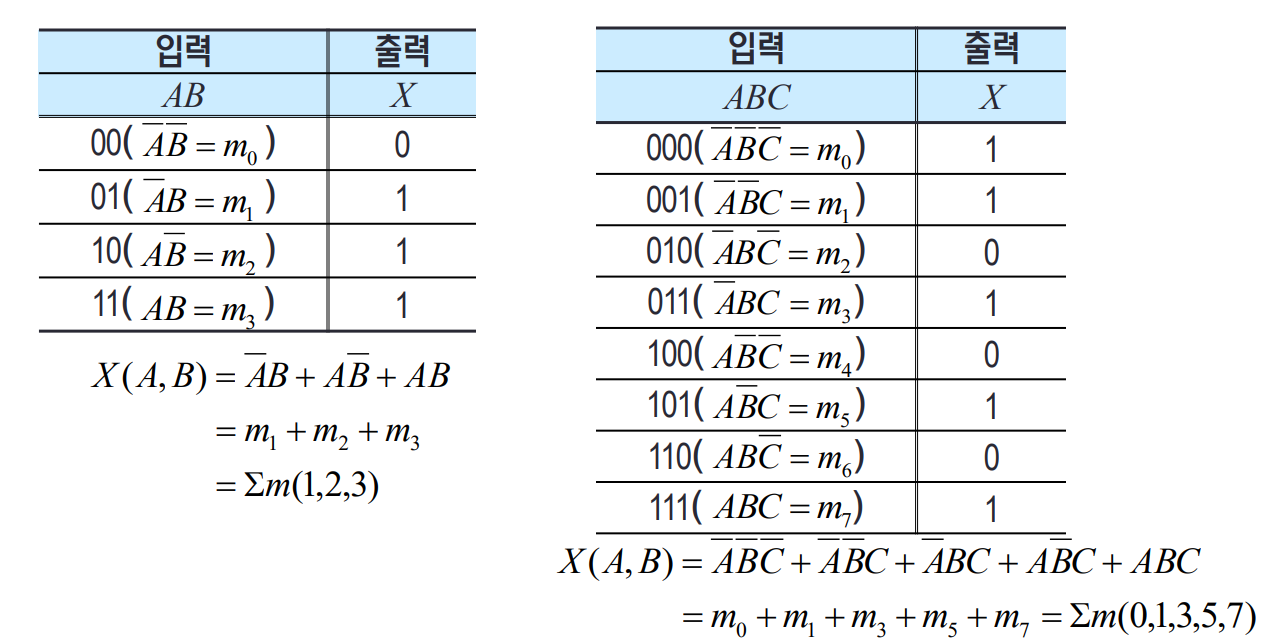
3-4. 최대항(Maxterm)과 POS(Product of sum, 합의 곱)
(1) 정의와 여러 가지 특징
- 최대항(Maxterm)은 표준 곱의 항, 즉 함수의 모든 변수를 포함하는 OR 항을 의미합니다.
- 최대항식은 출력이 0이 되는 각 항을 OR로 나타낸 후 AND 연산으로 결합합니다.
- 간소화 여부와 관계없이 OR-AND 식을 POS라고 합니다.
(2) 예시

3-5. 카르노 맵(Karnaugh Map)
(1) 정의와 여러 가지 특징, 간소화 방법
- 부울 함수를 간소화할 수 있는 또 하나의 방법으로써 복잡한 형태의 부울 함수를 시각적으로 도식화시켜, 간소화를 진행하는 방법입니다.
- 복잡한 형태의 부울 함수, 3개 이상의 변수를 가진 부울식을 간소화할 때 사용합니다.
- 5변수 이상의 부울식에 대해선 일반적으로 카르노 맵 방법을 사용하지 않습니다.
(SOP 기준)
- 도식화하여 각 항에 대한 값이 1인 칸들을 2의 n제곱 개로 묶습니다. (n =1, 2, 3, ...)
- 0에서 1, 1에서 0으로 변경된 변수들에 대해선 부울식에서 제외하고, 변하지 않는 변수들에 대해서만 0은 변수의 부정으로, 1은 변수 그대로 곱의 형태로 묶어서(AND) 더합니다(OR).
(2) 2변수 카르노 맵

(3) 3변수 카르노 맵
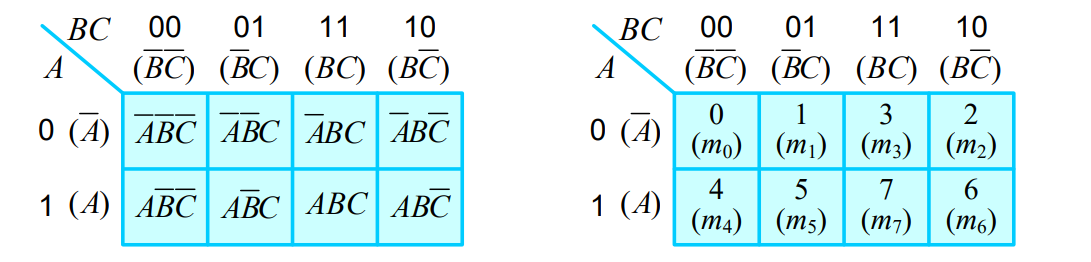
(4) 4변수 카르노 맵

4. 회로 실습 및 Simulation
4-1. [실험 1] - 보수기

(1) 회로도 구현
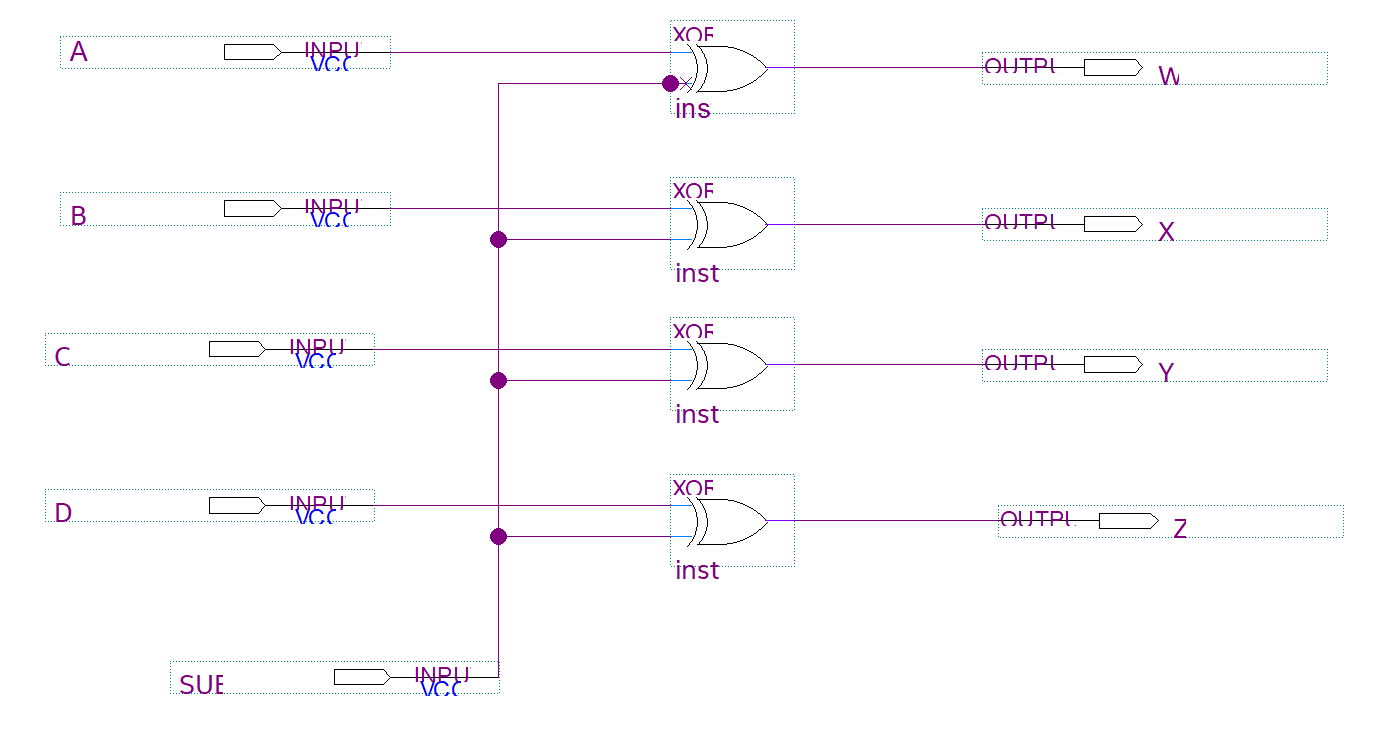
(2) Simulation

(3) 진리표(Truth table) 작성
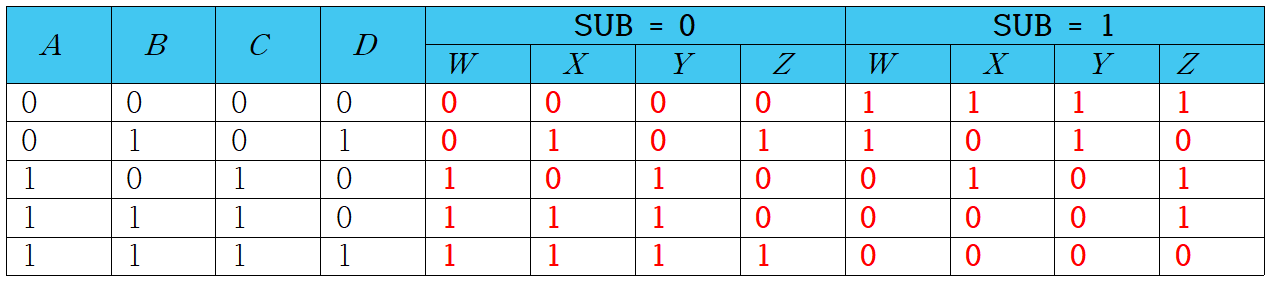
4-2. [실험 2] - 부울 함수 간소화(Simplification)


(1) 진리표 작성

(2) 부울함수 Y까지 포함하여 회로도 작성

(3) Simulation

- 학부에서 수강했던 전공 수업 내용을 정리하는 포스팅입니다.
- 내용 중에서 오타 또는 잘못된 내용이 있을 시 지적해 주시기 바랍니다.
